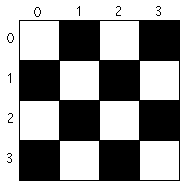


with n=2 (2n=4)
Please email your solution to the TA, at league@cs.yale.edu, with cs429hw3 in the subject.

|

|

|
| a board, with n=2 (2n=4) |
a tromino | a tiling |
It will be convenient to treat the origin (0,0) as the upper left corner of the board. Just for kicks, here is a larger tiling (with n=3):

Orientation: We need a representation of the four possible orientations of a tromino. Notice how the tromino's shape resembles an "arrow." We will describe a tromino's orientation by using the direction in which the arrow points. The four possible directions are specified by the following datatype declaration:
data Orientation = NW | NE | SW | SE
deriving Show
The diagram below should make each orientation clear.
 |
 |
 |
 |
| NW northwest |
NE northeast |
SW southwest |
SE southeast |
Location: We also need to specify a tromino's location on the board. We will do so using the coordinate of the "arrow point square," expressed as a pair of points (x,y) with type (int, int). The board's upper-left square has a coordinate value of (0,0).
For computing the board size, 2n, I suggest you define a function pow2 :: Int -> Int. The infix power operator in Haskell is (**), but it returns a Float, so you will need to convert it back to an Int.
Tromino representation: Thus, a tromino can be represented by its orientation and a pair of points indicating the coordinate of its "arrow point square." Such a representation can be expressed with the following declaration:
type Tromino = (Int, Int, Orientation)
We can represent a tiling of the board with a list of trominoes. For
example, the tiling seen at the beginning of this question can be
represented by the following list:
[(0,0,NW),(3,0,NE),(3,3,SE),(0,3,SW),(1,1,NW)]
The first helper function to write is the translate function, which takes an (x,y) offset and a tromino list. The function shifts each of the given trominoes by the given offset, returning the resulting list of trominoes.
translate :: (Int,Int) -> [Tromino] -> [Tromino]
For example, if given the offset (2,3) and the list of trominoes
[(1,1,SW),(3,3,NE)] and then
translate should return [(3,4,SW),(5,6,NE)].
Next we need to be able to flip the board about either axis. We will call these functions xflip and yflip. They will take the length of one side of the board as its first argument, then the list of trominoes. Each function returns the reflected tromino list.
xflip :: Int -> [Tromino] -> [Tromino]
yflip :: Int -> [Tromino] -> [Tromino]
The
difference between them is illustrated in the following figure.
 |
 |
 |
| t0 | xflip 4 t0 | yflip 4 t0 |
tile :: Int -> [Tromino]
import qualified SOEGraphics as G
Remember to use qualified names (such as G.xyz) to refer
to functions in the library.
The top-level function, render, will take the title of the window, a natural number n, and a list of trominoes. It will open a window and render the trominoes in different colors.
render :: String -> Int -> [Trom] -> IO ()
First we must choose how many pixels to dedicate to each square of the
board. I think 30 works well, but define this as a constant so it can
be changed easily.
-- pixels per square
pps = 30 :: Int
Here is a template for the render function:
render title n ts = G.runGraphics $
do w <- G.openWindow title (dim,dim)
...other rendering operations...
where dim = pow2 n * pps
We can use this to generate and render a tiling for a board of size
2n:
renderTiling :: Int -> IO ()
renderTiling n = render ("tile "++show n) n (tile n)
You will probably find it useful to define an infinite stream of colors. The graphics library defines G.colorList :: [(Color,RGB)] where Color is a data type with constructors named Red, Blue, and so on. RGB is a triple of 8-bit words. The first color in the list is Black. Thus, the following code produces an infinite stream of all colors except for black.
colors = tail (map fst G.colorList) ++ colors
Feel free to substitute your own colors -- once your renderer is
working!
I suggest rendering each tromino as a polygon. The library defines G.polygon :: [Point] -> Graphic for creating polygons from a list of points. Thus, the kernel of your program might be a function which generates polygon vertices for a given tromino:
trominoPolygon :: Tromino -> [Point]
You will probably want other helper functions, but the rest is up to
you. Try to make your code as concise and elegant as possible.
Congratulations. You have just reached the final round of the game show "The Winner Takes It All". All you have to do is to decide is if the order of a line up of items that is presented to you on a conveyer belt follows certain rules. The show master has already acquainted you with them ahead of time (they may vary from game to game) and you are very lucky today! There are only two rules he asked you to memorize.
V K V E TQuickly you see, that sure, that's ok, because the first
V and K satisfy two of the tree
requirements of rule 1. Note that rule 1 is not fully applied yet,
because there must be at least one entertainment item among the
remaining articles. The next V is valid by rule 2, then
comes E which justifies the application of rule 1. And
the final item T justifies the second rule. If this were
the real game and not just a practice round, you should have said
YES!.
V V TAs you can quickly see, this order of articles cannot be justified by the two rules from above. You should say NO, and the car, the bike, and the trip to Cancun would have been yours.
The conveyer belt starts rolling and you see
V K V E K EAlso this is a valid order, because it is justified by rule 1 (two applications) .
Back to the homework! Please solve this problem for the general case by writing a Haskell program which decides for you if to say yes or no.
type Rule = [Char]
play :: [Rule] -> String -> Bool
I am sure, that your solution will return an answer in less
time than 30 seconds. You can assume that the rules are formalized as
lists of characters [Char], and the items of the conveyer
belt are presented to you as a String.
Hint: Try to adopt and modify the code for matching regular expressions in class. Do not write more than 40 lines of code! If you do, something is likely to be wrong, or you haven't found an elegant solution.
With this problem we return to the world of algorithms that match regular expressions. In class we have discussed the standard set of operators of regular expressions, and we have discussed an algorithm that decides if a string is matched by a regular expression our not. You are asked to extend the regular expression language by a new constructors that can express negation.
acc "00" (Not (Star (Char "1"))) initshould succeed, because
00 is not an element of Star
(Char "1").
To solve this problem we extend the data type Reg by
the new constructor Not:
data Reg
= Zero
| One
| Char Char
| Plus Reg Reg
| Times Reg Reg
| Star Reg
| Not Reg
deriving Show
Mathematically, the language generated by this language is defined
as
L(Not R) = {s | s is not an element of L(R)}
Please extend the acceptor for regular expressions accpresented in class to cover this new case.